Introduction to metric measurements

In the study of science, measurement is very important, as it allows for precision and accuracy whether you are performing chemistry experiments or solving physics equations. It is also necessary in everyday life: you need measurements for baking and cooking, for hanging pictures, or for building things. Scientists use many different types of measurements, which can be confusing. This article will explain the most common measurements.

One Dimension: Length: It is easy to measure the length of a straight line on a piece of paper using a ruler. Objects that can easily be measured in one dimension, like a line, are measured in inches. If something is longer we measure it in feet, yards or miles. These are the measurements we use every day, but they aren’t really that easy to use. We have to memorize that there are 12 inches in a foot, three feet in a yard, and 5,280 feet in a mile.

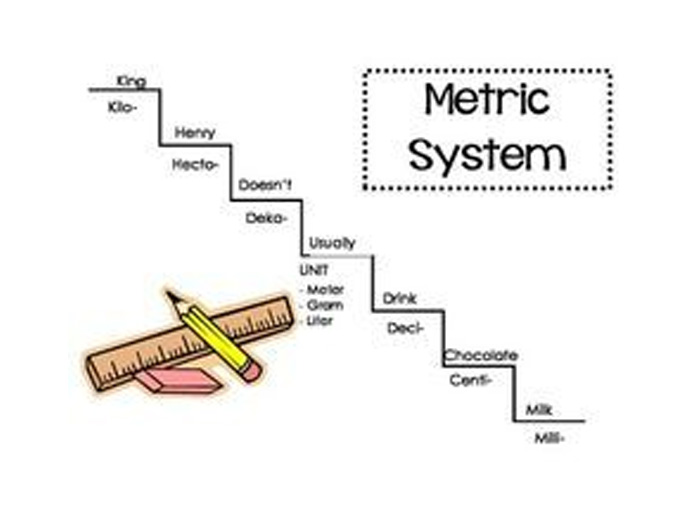
Scientists use a simpler measurement system called the metric system, where all the measurements are related to each other by a multiple of ten. The basic measurement in this system is called a meter (m). Use a tape measure to see how long 39 inches is; that’s the length of a meter. A centimeter (cm) is used to measure shorter lengths. There are 100 centimeters in a meter. (The prefix centi– in Latin means one hundred.) An even smaller measurement is a millimeter (mm), which is equal to the thickness of a dime.

There are 10 millimeters in a centimeter and 1000 millimeters in a meter. Milli- means thousand in Latin. For long distances, the metric system uses a kilometer (km), which is exactly 1,000 meters.

Two Dimensions: Area: It is a bit harder to calculate the dimensions of a square, isn’t it? The space inside a square (or other shape) is called area. To calculate area we need to take two measurements (you can remember this because a square is two-dimensional). Its area equals the length of its base times the length of its height. The units we use for area are typically in2 or cm2 (pronounced ‘square inches’ or ‘centimeters squared’). For example, if a square has sides that are 10 cm long, the area is 10 cm x 10 cm = 100 cm2.

Three Dimensions: Volume: For 3D objects, we calculate volume, which is how much total space the object takes up. To visualize what volume is, suppose you have a perfectly square container (length, width, and height all equal), and there is an opening at the top so you can pour water in. If you fill the container to the top, you will have a cube of liquid inside the container.

The space the liquid takes up is the volume of the container. You could measure the amount of liquid in the cube to find the cube’s volume. The units of measurement for liquid volume are ounces, cups, quarts, and pints. In the metric system the standard measurement for liquid volume is a liter (l). Smaller amounts are measured in milliliters (ml). Remember that milli- means one thousand: there are 1000 milliliters in a liter.

But what if the cube is solid? How can you measure its volume? You take three measurements (remember, a cube is three-dimensional) and multiply them together. Length x Width x Height = Volume. If the cube has sides 10 cm long, the volume would be 10 cm x 10 cm x 10 cm = 1000 cm3(pronounced as cubic centimeters).